保罗?萨缪尔森曾说过,“要想在现代社会做一个有文化的人,你必须对博弈论有一个大致了解”。事实上,不论是否了解博弈论,在波云诡谲的商业竞争局中、在风云变色的政治角力场里,各自发力的个体与个体、群体与群体甚至个体与群体,无一不在相互博弈。

每一个博弈都是你中有我、我中有你的情形。不同的博弈参与者,可以选择不同的行动,但由于相互作用,一个博弈参与者的利益不仅取决于自己采取的行动,也取决于其他博弈参与者所采取的行动。博弈论的精髓在于基于这种策略性相互依赖基础上的理性换位思考,即在选择你的行动时,还是考虑你的得益,但是你应当用他人的得益去推测他人的行动,从而选择最有利于自己的行动。也就是说,博弈论其实是关于有理性且利益关联的各方在竞争性活动中制定最优策略的理论,是一种有关“互动行为”的科学。
8月12日、13日 、18日和19日,在EMBA的课堂上,上海国家会计学院创院院长夏大慰教授带领着学员们一窥“博弈论”的门径。
智者之虑??有限重复博弈中的“逆向归纳”
有限次重复博弈是指相同结构的博弈有限次重复进行。当参与方确切地知道一个重复博弈什么时候结束时,所谓的期末问题就出现了。由于无法在最后一次对对手违背协议行为进行惩罚,因此参与方就会采取如同一次博弈的策略??不合作的欺骗或违约。
在有限次重复博弈中,人们往往可以利用逆向归纳法,即向前展望,向后推理来进行判断。夏教授举了“村庄大屠杀”的例子:在一个古老的母系氏族村落中有100对夫妻,如果男方不忠即会被女方杀死。不幸的是,在这个村子里所有的男人都对他们的妻子不忠,而村里每个男人的不忠除他的妻子外的99个女人都知晓这一事实。一位老妇人的到来打破了村子表明上的平静,老妇人告诉所有人“村子里的100个男人至少有一个对自己的妻子不忠”。老妇人说完离开后,村子里平静地过去了99天,当第100天降临时,所有的男人都被他们的妻子杀了。试想一下,当老妇人一语激起千层浪的时候,100个女人都不确定自己的丈夫是否对自己不忠,但是99天过去了,其他女人都没有杀了自己的丈夫,这时候所有女人都明白了,自己的丈夫就是这“至少一个对自己的妻子不忠”的人。
为了让学员们尝试在有限重复博弈中自行逆向归纳,夏教授请了五位学员上台做了一个“海盗分金币”的游戏。5个海盗劫船抢得100枚金币,他们按抽签的顺序(将海盗编为1号、2号、3号、4号和5号)依次提方案:首先由1号提出分配方案,然后5人表决,包括自己在内超过半数同意方案通过,否则他将被扔入大海喂鲨鱼,依此类推。学员们普遍认为,顺序为先的海盗不具优势,尤其1号海盗简直是必死无疑,认为提出的方案自己少拿甚至不拿金币才有可能保命。当夏院长揭开谜底时,1号海盗出乎意料地是最具先发优势的人,他不但可以消除死亡威胁,还可以成为收益最大的赢家。
具体的推理过程是这样的:
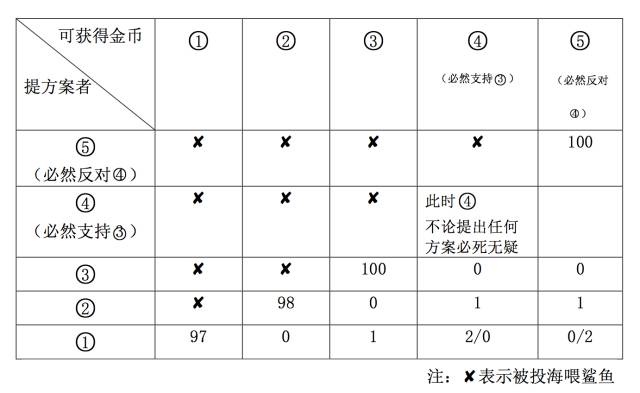
从后向前推导,如果1至3号强盗都喂了鲨鱼,只剩4号和5号的话,5号一定投反对票让4号喂鲨鱼,以独吞全部金币。所以,4号惟有支持3号才能保命。
3号知道这一点,就会提出“100,0,0”的分配方案,对4号、5号一毛不拔而将全部金币归为已有,因为他知道4号一无所获但还是会投赞成票,再加上自己一票,他的方案即可通过。
不过,2号推知3号的方案,就会提出“98,0,1,1”的方案,即放弃3号,而给予4号和5号各一枚金币。由于该方案对于4号和5号来说比在3号分配时更为有利,他们将支持他而不希望他出局而由3号来分配。这样,2号将拿走98枚金币。
同样,2号的方案也会被1号所洞悉,1号并将提出(97,0,1,2,0)或(97,0,1,0,2)的方案,即放弃2号,而给3号一枚金币,同时给4号(或5号)2枚金币。由于1号的这一方案对于3号和4号(或5号)来说,相比2号分配时更优,他们将投1号的赞成票,再加上1号自己的票,1号的方案可获通过,97枚金币可轻松落入囊中。这无疑是1号能够获取最大收益的方案了。答案是:1号强盗分给3号1枚金币,分给4号或5号强盗2枚,自己独得97枚。分配方案可写成(97,0,1,2,0)或(97,0,1,0,2)。
在一般的认知中,会有一个“先分者倒霉”的思维定式??游戏时学员们普遍认为1号难以逃脱落入鱼腹的悲剧。这就好像在商业竞争中,面对未知的市场“蓝海”,第一个吃螃蟹的先行者往往面临最大的风险。但如果他能用博弈的思维,牢牢把握住先发优势,结果不但消除死亡的威胁,还能获得最大的收益。而4号和5号,看似最安全,没有死亡的威胁,甚至还能坐收渔人之利,却因为失去主动权而只能看别人脸色行事,能否分得一小杯羹也完全取决于1号的决断。
达者所规??无限重复博弈中的“合作共谋”
无限次重复博弈则是指同一个博弈被无限次重复多次。和有限次重复博弈不同,当无限博弈重复没有确定的“终结之日”时,合谋作为纳什均衡就可以维持下去。从背叛行为的收益和成本来考虑,在无限次重复博弈中,当前收益小于等于未来收益的现值,背叛行为是没有好处的。原因在于,在这样的博弈中,各方是秉持着一种触发策略的,即视对方上一阶段的博弈行为决定自己下一阶段的策略是选择合作还是不合作。且双方从合作开始,如果某一阶段一方采取背叛,那么另一方在下一阶段开始永远用背叛来惩罚他(冷酷策略)。总体来说,双方其实都是从“以牙还牙”策略出发考虑的,从合作开始,在以后每天(每个阶段)里,如果对方选择合作,那你继续和他合作。如果对方在某一阶段采取背叛策略,则你在随后阶段也采取背叛策略来报复他。比如,如果对手在过去没有做过广告,那我就不做;一旦对手做广告,我也用高强度的广告来惩罚他。但是如果对方在下一阶段回心转意,又采取合作策略,那么你在再下次继续博弈中还是可以选择和他合作。事实上,只要对手在过去没有过“欺骗”行为,各个企业都会同意“合作”。因为欺骗行为只会引发后续阶段的惩罚。当然,这需要有四个前提:
有能力监督对手的行动;
有惩罚叛徒的能力和名声;
低利率;
在未来进行博弈的机会多。
在这样的前提下,企业数量少时比企业数量多时更容易实现合谋。1950年,美国市场有三家公司生产涡轮发电机:通用电气 公司最大,占有大约60%的市场份额;其次是西屋电气公司,占大约30%的市场份额;爱科公司则占10%的份额。 它们采用了一种很精明的协调方法,来维持各自的占有率,并获得高价。电力公共事业为打算购买的涡轮发电机招标。如果招标在历月的1至17日发布,西屋和爱科必须各自提交一个非常高的竞价,且该竞价必定失败,这样,通用就会以最低的竞价(但仍是可获得高额利润的垄断价格)成为合谋推举出来的胜出者。类似地,如果招标是在18至25日发布的,西屋就是指定胜出者,而爱科则是26至28日的指定胜出者。由于电力公共事业并不根据月历发布他们的招标计划,因而久而久之,每家生产商都得到协议的市场份额。任何违背协议的公司很快就会被对手发现。通用电气、西屋电气和爱科公司无疑都无限重复博弈中寻找到了一个最优策略,达成了纳什均衡。
但是值得一提的是,根据谢尔曼反托拉斯法案第二节,合谋是违法的。在“涡轮机阴谋”中,最终司法部门找出了三家公司投标的规律,三家公司的执行总裁都难逃锒铛入狱的命运。虽然如此,无限重复博弈中这种考虑长期回报、拒绝短期机会主义利益的思路还是很值得我们重视并借鉴于实际的商战中。
智慧领先于时间,结果发生于事件之前
夏教授在课堂上给予了学员们充分的思考与讨论空间,他提出了几个问题,要求学员们活学活用,将博弈论运用到实际问题的解决中。
夏教授抛出的第一个问题是:有时,我们会在街头上看到乞讨的残疾儿童。遇到这种情况时,你会施舍吗?为什么?
针对这一问题,第五组的学员给出了他们的答案。小组代表坦言,在讨论过程中大家是有不同看法的。但大多数成员在回答这个问题时会考虑两个维度??施舍者在施舍后都得到了良心安慰(+1),反之,不施舍则受到良心谴责(-1);广义上的儿童(并不是指被施舍的儿童而是指对儿童这个整体),假设这些乞讨的儿童绝大多数不是天生残疾而是犯罪机构使他们后天致残以求得利益的一种变态商业行为,那么在获得施舍的情况下,广义上的儿童受到的是一种巨大的负面效应,相应的会打出绝对值非常大的负分(-10),反之不施舍则会抑制这种变态而不人道的商业行为(10)。所以,基于以上得出的最优反应是不施舍。
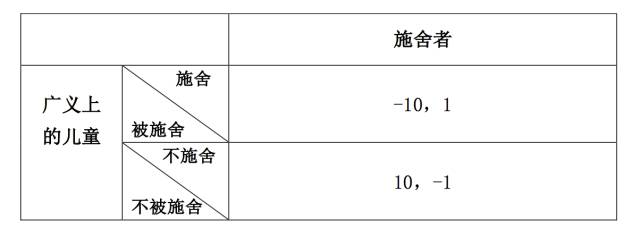
当然,组内还有部分成员认为,如果仅对当下乞讨的儿童来说,结论是相反的。
有其他小组的组员提出了自己的看法,认为残疾儿童乞讨从本质上就是一种趋利行为。否则无抚养自身能力的儿童有需求应当求助于社会机构而不是选择“乞讨”的方式。
而后,夏教授继续鼓励学员们进行头脑风暴:为中小学生繁重的课业减负,已经呼吁了很多年,但为什么收效甚微?

EMBA15期学员、上海俊星国际教育投资管理股份有限公司董事长李俊的回答让人印象深刻,她认为这是一个当今社会最受关注的问题,教育部门呼吁了这么多年,要求学校给予学生减轻课业负担,不但没有减下来,反而“负负得正”。她坦言,作为家长也不想孩子那么累,也想孩子有更多的玩耍时间,也明白给孩子自由空间对儿童的健康身心发展很重要,作为家人陪孩子去学习也非常辛苦,整个周末都辗转在各类培训机构,但是心里想:别人会的,自己的孩子一样也不能拉下,抱着望子成龙、望女成凤的心态,一定不让孩子输在起跑线上,不愿落后与别人。从博弈论的角度来看:作为家长,从孩子一出生,潜意识里就在让孩子和其他同龄人攀比,你给孩子多学点,学的早,孩子就有很大期望考入好的学校,进入好的班级,将来起点比其他孩子要高,一旦进去好的小学,才有机会进入好的高中,好的高中才能考上名牌大学,将来出入社会也会有个好的工作。若是不给孩子额外加餐,任其自由发展,相比较其他孩子来说,孩子一定会在短时间内落后于别人,但是将来等他们慢慢长大,有些天赋比较好的孩子可能会有更好的造化,但是对于大多数普通的孩子来说,他所面临的一环扣一环的升学压力、社会竞争都比较大,进入个普通学校,学个普通的专业,将来做个普通的人。作为培训行业的资深从业者,她从08年创业做艺术培训和学前教育,可以说亲眼目睹了家长对课外培训态度的转变??从最初家长给孩子报个班要考虑考虑,到现在家长已经认可课外培训的重要性,在补习学科类课程之外,也会让孩子参加艺术类学习,这是社会教育了家长,希望孩子不仅要有好的学习能力,也要具备各类技艺类的竞争力,培养个全能的孩子。
最后讨论的是一个夏教授也认为“非常难”的问题:边缘政策对认识朝核问题有什么启示?
对于这个问题不少学员一直持续关注并且深有感悟。
上海美应管理咨询有限公司总经理江河首先抛出了自己的观点,他认为朝核问题表面上是美国和朝鲜的博弈??朝鲜想政权稳定延续,美国不希望朝鲜拥核,打破地区力量平衡。但其实深刻影响着周边的中国、韩国、俄罗斯、日本的安全和利益。就目前的状态来讲,各方倾向采用边缘政策,避免失控,所以保留余地和后路。目前的状态就是平衡点,但中国应适度强硬,美国应适度缓和给予朝鲜一定国际空间,朝鲜应适当放缓,避免触动大国神经。
上实融资租赁有限公司大项目二部总经理顾景刚则认为朝核问题是利益集团之间的博弈,更是利益集团利益交换、利益互动的结果。朝鲜在92年前苏联解体之后,最重要的能源供应渠道被剪断,并且在97、98、99年及随后的5年里,不同程度地遭受了重大的旱灾、水灾、病虫灾等。一直到现在粮食生产从未达到过92年以前的水平,产量只达到原来最好年份的6-7成。而且美国又将朝鲜的贸易通道、美元结算通道、以货易货通道等全面封堵。朝鲜在此种背景下刻意激化矛盾,造成核安全、核扩散等问题,通过此种极端手段,来获得美国以及中国等国的安慰和补偿。这也是朝核问题的根源之一,朝鲜正是以此为博弈,通过高调的威胁、极端的手段,追求能形成博弈的优势。但这样的博弈是不可持续的,因为他无法永远站在平衡点上。从长期的发展来看,它可能终究会在利益集团更高层面的博弈中,充当筹码、充当博弈中的利益交换品。
上海复旦微电子集团股份有限公司副总经理曾昭斌对这一问题更是颇有钻研。他详细分析了美国、朝鲜、中国、俄罗斯、日本和韩国“六方”的底线与期望,目前最可行也是最可能发生的情况就是美国手术刀式打击朝鲜,政权不更替。如果朝鲜报复,则触犯了韩国和日本国内不能产生重大伤亡的底线。如果朝鲜陷入乱局,则触犯了中国主权和领土不容分割以及朝鲜不能有难民问题两条底线。当然,如果打击完什么都不发生,皆大欢喜。但是这样最好的方案还要冒着盟国遭受大量伤亡的风险,所以现在各国普遍僵持,且一段时间内这样的情况很难改变,只要朝鲜离核武器小型化还有距离,大家可以允许这个事态继续僵持,毕竟也没什么好办法。
夏教授肯定了的认真思考、活跃讨论和多样性思维。他指出,之所以同学们常常会对一个相同的问题得出各异的结论,是因为考量问题的要素迥异、对要素的权重和正负判断也不同。从策略互动的角度来说,真正的好策略应当站在对方的角度考虑,从而优化自身的策略,从而实现纳什均衡。
2005年的诺贝尔经济学奖获得者托马斯?谢林曾说过,“一种策略性行为就是某人通过影响其他人对自己行为的预期,来促使其他人选择对自己有利的策略,是某人通过限制自己的行为来限制其对局者的选择”。作为博弈方,你不应该仅仅只是个被动的参与人,满足于接受别人制定的博弈规则,而应该设法改变博弈,使其对自己尽量有利。执行的承诺能够促进长期利润,但承诺方也确实因此而对自己的行动施加了严格的限制。这种通过限制自己行动来获取竞争优势的做法被称为策略性行为。通过策略互动最终实现纳什均衡是博弈论的精髓所在。
须知,真正善用博弈论者,他的智慧是可以领先于时间,看到发生于事件之前的结果的。(出自《博弈圣经》“智慧领先于时间,结果发生于事前”。)







